Potentiel érosif de la pluie : identification du meilleur estimateur d’énergie cinétique de la pluie à partir des données de Drop Size Distribution (DSD) de pluies mesurées au nord-ouest du Bénin

http://dx.doi.org/10.46411/jpsoaphys.2020.02.17

Section  de la parution:  Informations de publication

 

J. P. Soaphys, Vol 2, N°2 (2020) C20A17

Pages :  C20A17-1  à C20A17-5

DOI du journal   : https://doi.org/10.46411/jpsoaphys.journal
DOI du Numéro : https://doi.org/10.46411/jpsoaphys.journal.v2.2
DOI de l’article  : http://dx.doi.org/10.46411/jpsoaphys.2020.02.17
Print ISSN: 2630-0958
Historique de la version : actuelle
 
Copyright & Usage: 
Copyright © 2020,

Informations sur les auteurs

 Adjikpe Loïc Saturnin 1, 2, Moumouni Sounmaïla2, Kougbeagbede Hilair 1, Massou Siaka 1,

1 Laboratoire de Physique de l’Atmosphere, Université d’Abomey Calavi, Cotonou, Bénin,

2 Ecole Normale Supérieure de Natitingou, Université Nationale des Sciences, Technologies, Ingénierie et Mathématiques, Natitingou, Bénin

 Corresponding author e-mail: adjikpel@gmail.com

 

RESUME

Le potentiel érosif de la pluie est sa capacité à provoquer l’érosion du sol. Son étude s’appuie sur l’énergie cinétique (KE) de la pluie qui peut être obtenue à partir de la distribution granulométrique des gouttes de pluie (en anglais Drop Size Distribution : DSD). Ce travail propose deux estimateurs de l’énergie cinétique de la pluie (KE) au Nord-Ouest du Bénin, l’un à partir de l’intensité de pluie (I) et l’autre à partir du facteur
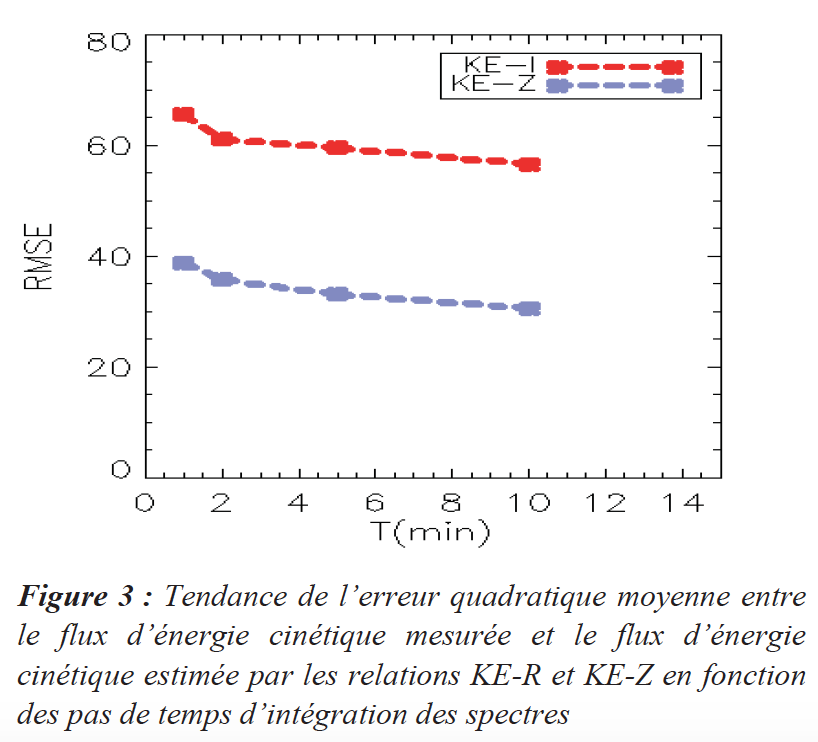
de réflectivité radar (Z) dans l’approximation de Raleigh. Les deux relations climatologiques KE-I et KE-Z sont établies à partir des données de DSD mesurées sur trois sites au Nord-Ouest du Bénin. L’énergie cinétique de la pluie a été évaluée par l’utilisation des relations KE-Z et KE-I. Ainsi, il est noté que la relation KE- Z est plus performante que la relation KE – I. Par ailleurs, en évaluant la sensibilité de ces relations KE – I et KE – Z au pas de temps d’intégration des spectres de DSD, il ressort que la performance de ces relations augmente avec le pas de temps d’intégration.

Mots-Clés : DSD – Taux de pluie – réflectivité radar – énergie cinétique – potentiel érosif

Van Dijk, I.J.M.; Bruijnzeel, L.; Rosewell, C., 2002. ‘’Rainfall intensity–kinetic energy relationships: A critical literature appraisal’’, J. Hydrol., 261, 1–23.

Fornis, R. L., H. R. Vermeulen, and J. D. Nieuwenhuis, 2005. ‘’Kinetic energy-rainfall intensity relationship for Central Cebu, Philippines for soil erosion studies’’, J. Hydrol., 300, 20–32.116

Carollo, F.,G.; Ferro, V.; Serio, M.,A.,2017. ’’Reliability of rainfall kinetic power-intensity relationships’’, Hydrol. Process., 31, 1293–1300.
Fox, N.,I., 2004.’’TECHNICAL NOTE: The representation of rainfall drop-size distribution and kinetic energy’’, Hydrol. Earth Syst. Sci., 8, 1001–1007. Mineo C. and Elena Ridolfi, 2019.’’Assessment of rainfall kinetic-energy–intensity relationships’’, J.water, MDPI., 2019, 11,16 18.1994
Jan Pétrù and Jana KALIBOVÁ, 2018. ‘’measurement and Computation of Kinetic Energy of Simulated Rainfall in Comparison with Natural Rainfall’’, Original Paper Soil & Water Res.,13,(4):226–233. https://doi.org/10.17221/218/2016-SWR
Nan Yu, B.,Boudevillain and G., Delrieu, 2012.‘’Estimation of rain kinetic energy from radar reflectivity and/or rain rate based on a scaling formulation of the raindrop size distribution’’, Water Resources Research, vol. 48, w04505, doi:10.1029/2011wr011437.
Steiner M., Smith J.A. Reflectivity, 2000. ‘’Rain rate, and kinetic energy flux relationships based on raindrop spectra’’. Journal of Climate and Applied Meteorology., 39: 1923–1940.
Redelsperger, J.,L.,C.; Thorncroft, A. ; Diedhiou, T.; Lebel, D, 2006, ‘’Parker, and J. Polcher. African Monsoon, Multidisciplinary Analysis (AMMA)’’, An International Research Project and Field Campaign: Bull. Amer. Meteor. Soc., 88, 1739-1746. Atlas, D., and C.,W.,Ulbrich., 1977. ‘’Path and areaintegrated rainfall measurement by microwave attenuation in the 1-3 cm band’’. J. Appl. Meteor., 16, 1322-1331.
Moumouni S., Gosset M., and Houngninou E., 2008, Main features of rain drop size distributions observed in Benin, West Africa, with optical disdromètres: Geophys. Res. Lett. 35: L23807, DOI:10.1029/2008GL035755.
Moumouni S., 2009, Analyse des distributions granulométriques des pluies au Bénin : caractéristiques globales, variabilité et application à la mesure radar, Thèse de Doctorat, INP-Grenoble.
Kinnell, P., 1987. Rainfall energy in eastern Australia– Intensity kinetic energy relationships for Canberra, ACT. Australian Journal of Soil Research, 25 (4), 547–553. doi:10.1071/SR9870547 [Crossref], [Web of Science ®], [Google Scholar]
Sauvageot, H., 1982. « Radarmétéorologie. Télédétection Active de l’Atmosphère », Eyrolle,Paris, 296 p.
Nash, J., E. and J.,V., Sutcliffe, 1970. ‘’River flow forecasting through conceptual models part I – A discussion of principles’’, J. Hydrol.,10, 282-290.
Chapon B., Delrieu G. and Gosset M.,2008, ’’Variability of rain drop size distribution and its effect on the Z–R relationship: A case study for intense Mediterranean rainfall,’’ J. Atmospheric Research 87 (2008) 52–65

article elements

images

Categories: