Étude de l’effet du taux de dopage et de l’épaisseur des couches antireflets sur les paramètres électriques des photopiles au silicium
- Post by: SOAPHYS-KZ
- 27 décembre 2025
- Comments off

http://dx.doi.org/10.46411/jpsoaphys.2021.C25.14
Section de la parution: Informations de publication
J. P. Soaphys, Vol 5, N°2 (2025) C25A14
Pages : C23A14-1 à C25A14-7
Informations sur les auteurs et affiliations
Papa Mass Seck1, Sada Traore1,2, Moussa Camara1,3, Thiar Diop4, Moustapha Thiame1*
1Laboratoire de Chimie et de Physique des Matériaux (LCPM), Université Assane Seck de Ziguinchor, Diabir, BP 523 – Ziguinchor – Sénégal,
2Laboratory of Semiconductors and Solar Energy, Physics Department, Faculty of Science and Technology, Cheikh Anta Diop University, Dakar, Senegal
3Faculté des Sciences, Université Gamal Abdel Nasser de Conakry, Conakry, République de Guinée
Corresponding author e-mail : mthiame@univ-zig.sn
RE S U M E
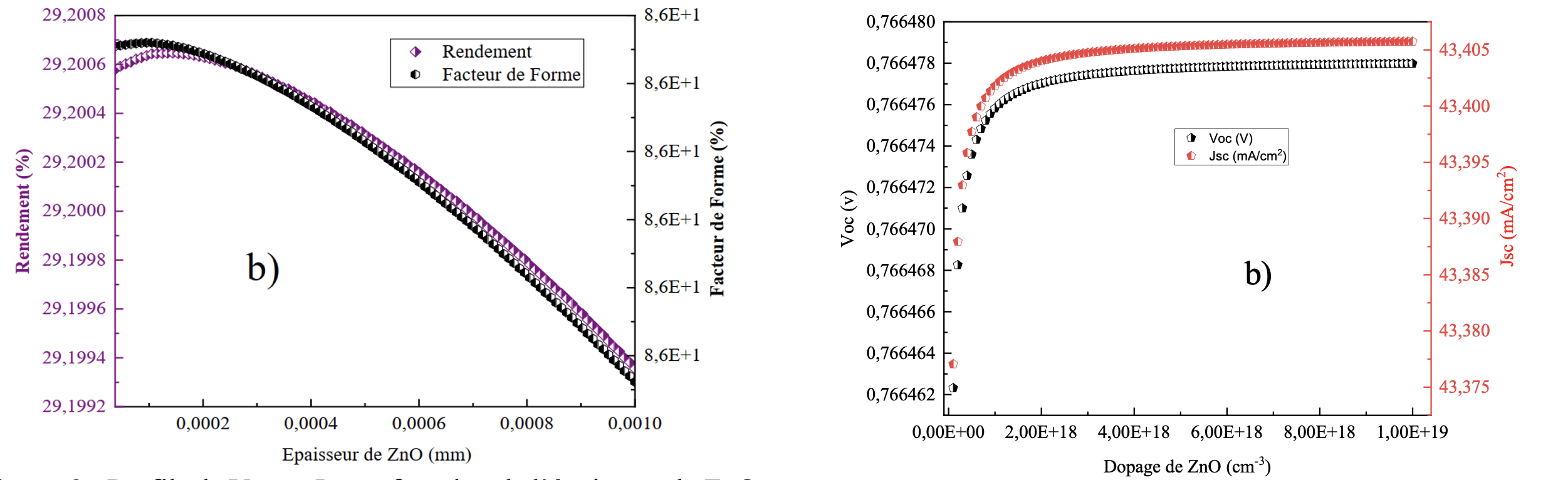
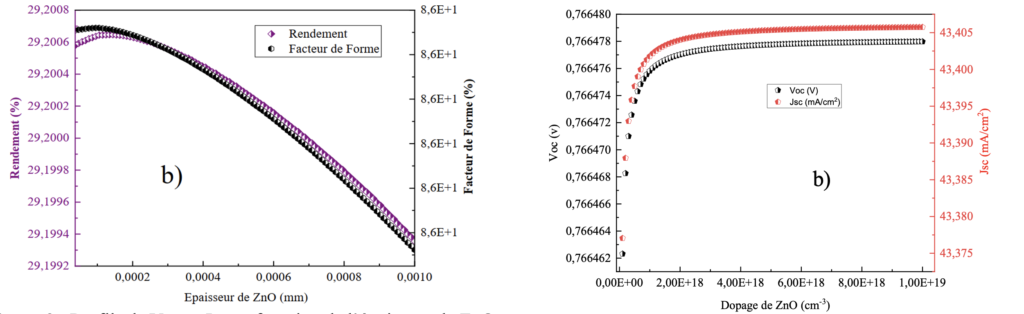
Cette étude vise à optimiser l’efficacité des cellules solaires de type Si(n)/Si(p) par une ingénierie précise de la couche Antireflet (ARC). Nous avons analysé l’influence de deux paramètres cruciaux : l’épaisseur et le taux de dopage sur les propriétés électriques et optiques de trois matériaux ARC sélectionnés : ZnO, SnO2 et Al0.3Ga0.7As. La méthodologie d’optimisation a révélé que la performance du dispositif repose sur un équilibre délicat. D’une part, l’augmentation du taux de dopage a un impact positivement dominant sur les propriétés électriques en augmentant la conductivité et en réduisant la résistance série (Rs), améliorant ainsi le FF et le rendement. D’autre part, l’augmentation de l’épaisseur est limitée par un optimum strict ; au-delà de ce point, elle influence négativement les performances en perturbant l’effet antireflet (chute de Jsc) et en augmentant Rs (chute de FF et Voc). La comparaison des matériaux a clairement désigné le ZnO comme la couche ARC la plus performante. L’optimisation a permis au dispositif Si(n)/Si(p) d’atteindre le meilleur rendement (ηmax≈ 29,20 %) pour le ZnO à une épaisseur de 124 nm et un taux de dopage de 2×1018 cm−3.
Mots-Clés : Taux de dopage, Epaisseur optimal, Couche antireflet, Paramètres électriques optimaux
A B S T R A C T
This study aims to optimize the efficiency of Si(n)/Si(p)-type solar cells through the precise engineering of the Anti-Reflection Coating (ARC). We analyzed the influence of two crucial parameters: thickness and doping concentration on the electrical and optical properties of three selected ARC materials: ZnO, SnO2, and Al0.3Ga0.7As. The optimization methodology revealed that device performance relies on a critical balance. On one hand, increasing the doping concentration has a positively dominant impact on electrical properties by boosting conductivity and reducing series resistance (Rs), thereby improving the FF and efficiency. On the other hand, increasing the thickness is constrained by a strict optimum; beyond this point, it negatively affects performance by disrupting the anti-reflection effect (drop in Jsc) and increasing Rs (drop in FF and Voc). Material comparison clearly identified ZnO as the most performing ARC layer. The optimization allowed the Si(n)/Si(p) device to achieve the best efficiency (ηmax≈ 29.20 %) for ZnO at a thickness of 124 nm and a doping concentration of 2×1018 cm−3.
Keywords : Doping rate, Optimal thickness, Anti-reflective layer, Optimal electrical parameters
REFERENCES
[1] REN21,
Renewables 2024 Global Status Report, 2024.
[2] Márquez, C. R. (2025) Solar-Grade Silicon in
the Energy Transition: A Strategic Commodity for the Global Photovoltaic
Market. Commodities, 4(3),
18. https://doi.org/10.3390/commodities4030018
[3] Sene, M., Samoura, A., Diouf, S., Diao, A.
and Mbow, C. (2023) Electrical Modeling of a Silicon Photovoltaic Solar Cell:
Comparative Study of Models Characterizing the Photovoltaic Solar Cell. Open
Journal of Applied Sciences, 13, 1787-1795. doi: 10.4236/ojapps.2023.1310141.
[4] Sow, O. , Ba, M. , El Moujtaba,
M. , Traore, Y. , Sow, E. , Sarr, C. , Diop, M. and Sissoko, G. (2020)
Electrical Parameters Determination from Base Thickness Optimization in a
Silicon Solar Cell under Influence of the Irradiation Energy Flow of Charged
Particles. Energy and Power Engineering, 12, 1-15.
doi: 10.4236/epe.2020.121001.
[5] Traore, S., Diedhiou, A., Sambou, A. and
Camara, M. (2024) Study of the Electrical Parameters of a Silicon Solar Cell
(n+/p/p+) under the Effect of Temperature by Optimization of the Base Thickness
and the Doping Rate. Journal of Materials Science and Chemical Engineering,
12,15-23. https://doi.org/10.4236/msce.2024.1211002
[6] Sadio, O. , Kouyaté, M. , Traoré, P. and
Barro, F. (2023) Determination of the Electrical Parameters of a Solar Cell in
Steady State. Open Journal of Applied Sciences, 13, 1834-1843.
doi: 10.4236/ojapps.2023.1310144.
[7] Nordseth, Ø. , Kumar, R. , Bergum, K. , Fara,
L. , Foss, S. , Haug, H. , Drăgan, F. , Crăciunescu, D. , Sterian, P. ,
Chilibon, I. , Vasiliu, C. , Baschir, L. , Savastru, D. , Monakhov, E. and
Svensson, B. (2017) Optical Analysis of a ZnO/Cu2O Subcell in a
Silicon-Based Tandem Heterojunction Solar Cell. Green and Sustainable
Chemistry, 7, 57-69. doi: 10.4236/gsc.2017.71005.
[8] Gill, V. K., Juneja, S., Dixit, S. K.,
Vashista, S, and Kumar, S. (2024). Structural and optical properties of
phosphorous doped nanocrystalline silicon deposited using a VHF PECVD process
for silicon heterojunction solar cells and optimization of a simple p–n
junction cell using SCAP-1D tool. Royal society of chemistry, 14 ,
23873-23885.
DOI : 10.1039/D4RA02429J
[9] A. Cuevas, “The Effect of Doping on the
Recombination Lifetime of Silicon,” Solar Energy Materials & Solar Cells,
vol. 57, pp. 277–290, 1999.
[10] W. Shockley and W. T. Read. (1952)
Statistics of the Recombinations of Holes and Electrons, Physical Review,
vol. 87, pp. 835–842. https://doi.org/10.1103/PhysRev.87.835
[11] Bushick, K. and Kioupakis, E. (2023) Strain effects on
Auger–Meitner recombination in silicon”, Applied Physics Letters, vol.
123, n° 26. https://doi.org/10.1063/5.0176950
[12] Thiame, M., Camara, M., Lemrabott, H., Cheikh, M. L., Gueye, S and
Gregoire Sissoko, G. (2023). Étude a 3d de la photopile au silicium
polycristallin : optimisation du taux de dopage en fonction de l’épaisseur de
la base. International
Journal of Advanced Research, 11(12), 311-322. https://dx.doi.org/10.21474/IJAR01/17989
[13] A. Richter, M. Hermle, and S. W. Glunz.
(2012). Reassessment of the Limiting Efficiency for Crystalline Silicon Solar
Cells, Phys. Rev. B, vol. 86, Art. no. 165202. https://doi.org/10.1103/PhysRevB.86.165202
[14] Hwang, S. T., Kim, S., Cheun, H., Lee,
H.,Lee, B.,Hwang, T., Lee, S., Yoon, W., Lee, H.M and Park, B. (2016) Bandgap
grading and Al0.3Ga0.7As heterojunction emitter for
highly. Solar Energy Materials & Solar Cells, 155, 264–272.
http://dx.doi.org/10.1016/j.solmat.2016.06.009
[15] Mridha, S and Basak, D. (2006) Effect of
thickness on the structural, electrical and optical properties of ZnO films.
Materials Research Bulletin, 42, 875–882. DOI: 10.1016/j.materresbull.2006.08.019
[16] Mathiazhagan, G., Seeber, A., Gengenbach,
T., Mastroianni, S., Vak, D., Chesman, Anthony SR. A., Gao, M., Angmo, D and
Hinsch, A. (2020). Improving the Stability of Ambient Processed, SnO2-Based,
Perovskite Solar Cells by the UV-Treatment of Sub-Cells. RRL Solar, 4, 2000262.
https://doi.org/10.1002/solr.202000262
[17] Ozgur, U., Alivov, Y. I., Liu, C., Teke, A.,
Reshchikov, M. A., Dogan, S., … & Morkoç, H. (2005). A comprehensive
review of ZnO materials and devices. Journal of Applied Physics, 98(4),
041301. https://doi.org/10.1063/1.1992666
[18] Majumder, S., Krishnanunni, R. A and Ravindran, S. (2023) Optimization
of p-i-n GaAs/AlGaAs Heterojunction Nanowire Solar Cell for Improved Optical and
Electrical Properties. (2023) Journal of the Optical Society of America B,
40(10), 2684-2695. https://doi.org/10.1364/JOSAB.492196
[19] K. lagha-menouer .
(2011) Étude et réalisation d’une cellule solaire multicouches du type
Si-SiO2-SnO2-ZnO par APCVD”, Thèse Doctorat, Université Mouloud Mammeri de
Tizi-Ouzou.
[20] Wahari, I and Halidou, I.(2025) SCAPS-1D Numerical
Simulation of Homojunction and Heterojunction ZnO/Si Solar Cells. Asian Journal
of Physical and Chemical Sciences, 13(3), 55-67. DOI: 10.9734/ajopacs/2025/v13i3251
[21] Burgelman, M., Nollet, P and Degrave, N.
(2000) Modelling polycrystalline semiconductor solar cells. Thin Solid Films.
volume 361-362, 527-532. https://doi.org/10.1016/S0040-6090(99)00825-1
[22] Bachiri, B and Rahmoun, K. (2022) Numerical
simulation of perovskite solar cell with porous silicon layer. Desalination and
Water Treatment. 279, 136-139. https://doi.org/10.5004/dwt.2022.29098
[23] Park, H.-J., Son, H.,
& Jeong, B.-S. (2024). SCAPS-1D Simulation for Device Optimization to
Improve Efficiency in Lead-Free CsSnI3 Perovskite Solar
Cells. Inorganics, 12(4), 123. https://doi.org/10.3390/inorganics12040123.
[24] Abboudi, H.,
Belaid, W., En-nadir, R., Ez-zejjari, I., Zouini, M., Sali, A., & El Ghazi,
H. (2025). Optimization of InxGa1−xN
P-I-N Solar Cells: Achieving 21% Efficiency Through SCAPS-1D Modeling. Crystals, 15(7), 633. https://doi.org/10.3390/cryst15070633